Applications de la continuité
Applications de la continuité
I Continuité
Définition
Soit $f$ une fonction définie sur un intervalle I. Soit $a$ dans I.
$f$ est continue en $a$ si et seulement si $\lim↙{x→a}f(x)=f(a)$.
$f$ est continue sur I si et seulement si $f$ est continue en tout nombre $a$ de I.
Graphiquement, une fonction est continue quand le tracé de sa courbe représentative peut se faire sans lever le crayon.
Exemple
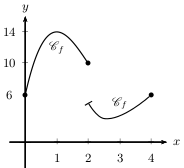
La fonction $f$ est continue sur l'intervalle $\[0;2\]$.
La fonction $f$ est continue sur l'intervalle $\]2;4\]$.
Mais la fonction $f$ n'est pas continue sur l'intervalle $\[0;4\]$ car elle est discontinue en 2!
Propriété
Soit $f$ une fonction définie sur un intervalle I. Soit $a$ dans I.
Si $f$ est dérivable en $a$, alors $f$ est continue en $a$.
Si $f$ est dérivable sur I, alors $f$ est continue sur I.
Définition et propriété
Les fonctions polynômes, la fonction valeur absolue, la fonction racine carrée, la fonction exponentielle,
la fonction logarithme népérien constituent les fonctions usuelles.
Les fonctions usuelles, ainsi que les fonctions obtenues par opérations ou par composition usant de fonctions usuelles,
sont continues sur les intervalles sur lesquels elles sont définies.
Exemple
La fonction $f(x)=(3x^2-5)e^{x-7}$ est-elle continue sur $\R$?
$f$ est définie sur $\R$.
Et $f$ est obtenue par opérations ou par composition de fonctions usuelles.
Donc $f$ est continue sur $\R$.
II Equations $f(x)=k$
Théorème des valeurs intermédiaires
Si $f$ est une fonction continue sur $\[a;b\]$,
Si $k$ est un nombre compris entre $f(a)$ et $f(b)$,
Alors l'équation $f(x)=k$ admet au moins une solution sur $\[a;b\]$.
Propriété
Par convention, dans un tableau de variation, les flèches indiquent évidemment que la fonction est strictement monotone, mais aussi qu'elle est continue.
Exemple
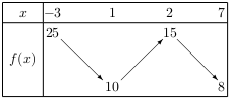
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=12$ admet au moins une solution sur $\[-3;7\]$.
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue sur $\[-3;7\]$.
Or, 12 est un nombre compris entre $f(-3)=25$ et $f(7)=8$,
Donc, d'après le théorème des valeurs intermédiaires, l'équation $f(x)=12$ admet au moins une solution sur $\[-3;7\]$.
Théorème de la bijection
Si $f$ est une fonction continue et strictement monotone sur $\[a;b\]$,
Si $k$ est un nombre compris entre $f(a)$ et $f(b)$,
Alors l'équation $f(x)=k$ admet une unique solution sur $\[a;b\]$.
 Exemple
Exemple
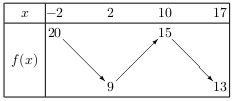
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=12$ admet exactement 2 solutions, la première entre -2 et 2, la seconde entre 2 et 10.
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement décroissante sur $\[-2;2\]$.
Or 12 est un nombre compris entre $f(-2)=20$ et $f(2)=9$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=12$ admet une unique solution $c_1$ sur $\[-2;2\]$.
De même, nous pouvons démontrer que l'équation $f(x)=12$ admet admet une unique solution $c_2$ sur $\[2;10\]$.
Enfin, comme 13 est le minimum de $f$ sur $\[10;17\]$, l'équation $f(x)=12$ n'admet pas de solution sur $\[10;17\]$.
Il est clair que: $-2$<$ c_1$<$2$<$ c_2$<$10$. L'équation $f(x)=12$ admet donc exactement 2 solutions, la première entre -2 et 2, la seconde entre 2 et 10.
Généralisation
Les théorèmes des valeurs intermédiaires et de la bijection s'étendent naturellement
à des intervalles semi-ouverts ou ouverts, bornés ou non.
Voir l'exemple ci-dessous.
 Exemple
Exemple
La fonction $f$ vérifie le tableau de variation ci-dessous.
Montrer que l'équation $f(x)=1$ admet exactement 1 solution sur $[-2,7;+∞[$.
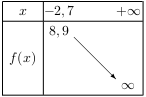
Corrigé
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement décroissante sur $[-2,7;+∞[$.
Or 1 est strictement inférieur à $f(-2,7)=8,9$, et $\lim↙{x→+∞}f(x)=-∞$.,
Donc, d'après le théorème de la bijection, l'équation $f(x)=1$ admet une unique solution sur $[-2,7;+∞[$.
A quoi peut servir le théorème de la bijection ?
On est parfois confronté à des équations difficiles à résoudre algébriquement. Il est alors tentant de lancer un programme qui permettra d'encadrer la solution recherchée. Mais encore faut-il qu'elle existe, et qu'elle soit unique sur l'intervalle d'étude !
Par application du théorème de la bijection, on est assuré que le programme nous donnera un résultat satisfaisant.
III Fonction réciproque
Définition et propriété
Si $f$ est une fonction continue et strictement monotone sur l'intervalle $I$,
alors l'ensemble des images $f(x)$ lorsque $x$ décrit $I$ est un intervalle $J$,
et, pour tout réel $k$ de $J$, il existe une unique solution $c$ dans $I$ à l'équation $f(x)=k$.
Cela définit alors une nouvelle fonction, appelée fonction réciproque de $f$, et notée $f^{-1}$, telle que,
pour tout $k$ de $J$, $f^{-1}(k)=c$ (où $c$ est l'unique solution de l'équation $f(x)=k$).
Propriété
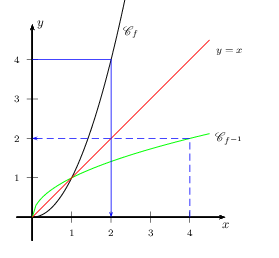
Dans un repère orthonormé, deux fonctions réciproques l'une de l'autre ont des représentations graphiques symétriques par rapport à la droite d'équation $y=x$
 Exemple
Exemple
On considère la fonction $f$ définie pour tout $x$ de $[0;+∞[$ par $f(x)=x^2$
Montrer que la fonction $f$ admet une réciproque $f^{-1}$ sur $[0;+∞[$ , et déterminer l'expression de $f^{-1}(x)$ pour tout $x$ de $[0;+∞[$. Tracer les deux courbes représentatives.
Corrigé
$f$ est continue et strictement croissante sur l'intervalle $[0;+∞[$. De plus $f(0)=0$ et $\lim↙{x→+∞}f(x)=+∞$.
D'où le tableau de variation:
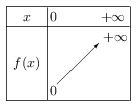
Par conséquent, l'ensemble des images $f(x)$ lorsque $x$ décrit $[0;+∞[$ est $[0;+∞[$,
et, pour tout réel $k$ de $[0;+∞[$, il existe une unique solution $c$ dans $[0;+∞[ $ l'équation $f(x)=k$.
On notera ici que: $f(x)=k$ $ ⇔$ $x^2=k$ $ ⇔$ $x=√{k}$ (car $x$ est recherché dans $[0;+∞[$ )
Finalement, la fonction $f$ admet donc une réciproque $f^{-1}$ sur $[0;+∞[$ , qui est telle que, pour tout $x$ de $[0;+∞[$ , $f^{-1}(x)=√{k}$
En résumé, les fonctions carrée (restreinte à $[0;+∞[$) et racine carrée sont réciproques l'une de l'autre.
Voici les tracés demandés. On notera que les représentations graphiques sont bien symétriques par rapport à la droite d'équation $y=x$
Les deux demi-paraboles sont parfaitement superposables par symétrie axiale.
On remarquera que, par exemple, $f(2)=4$ $ $⇔$ $ $f^{-1}(4)=2$