 Fonction logarithme népérien
Fonction logarithme népérien
Définition et propriété
La fonction logarithme népérien, notée $\ln$, est la fonction définie sur $]0;+∞[$ qui,
à tout réel strictement positif $b$ associe l'unique solution de l'équation $e^x=b$.
Ainsi, pour tout réel $b$ strictement positif, pour tout réel $a$, $a=\ln b⇔ e^a=b$.
Et par là, on obtient, en particulier:
$\ln 1=0$ $\ln e=1$.
Propriété
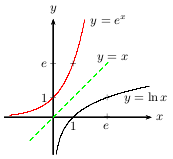
Dans un repère orthonormé, les courbes représentatives des fonction $\ln x$ et $^x$ sont symétriques par rapport à la droite d'équation $y=x$.
Dérivées
La fonction $\ln x$ admet pour dérivée ${1}/{x}$ sur $]0;+∞[$. Ainsi: $(\ln x)'={1}/{x}$
Soit $u$ une fonction strictement positive sur un intervalle I.
La fonction $\ln u$ admet pour dérivée ${u'}/{u}$ sur I. Ainsi: $(\ln u)'={u'}/{u}$
Les fonctions $u$ et $\ln u$ ont même sens de variation sur I.
 Exemple
Exemple
Soit $f$ définie sur $]0;+∞[$ par $f(x)=7\ln x+3x$.
Montrer que $f\,'(x)={7+3x}/{x}$.
Corrigé
$f\,'(x)=7{1}/{x}+3={7}/{x}+{3x}/{x}={7+3x}/{x}$. Exemple
Exemple
Soit $f$ définie par $f(x)=3x-\ln (2x-1)$.
Déterminer le domaine de définition $\D_f$ de $f$.
Calculer $f\,'(x)$, puis montrer que $f$ admet pour minimum $2,5-\ln{2}/{3}$ sur $\D_f$.
Corrigé
$f(x)$ existe si et seulement si $2x-1\text">"0$, soit: $x\text">"0,5$. Donc $D_f=]0,5;+∞[$.On pose $u=2x-1$, et donc $u'=2$.
Ici $f=3x-\ln u$, et par là $f\,'=3-{u'}/{u}$.
Donc $f\,'(x)=3-{2}/{2x-1}={3(2x-1)}/{2x-1}-{2}/{2x-1}={6x-3-2}/{2x-1}={6x-5}/{2x-1}$.
Le signe de $f\,'$ et le sens de variation de la fonction $f$ sont donnés ci-dessous.
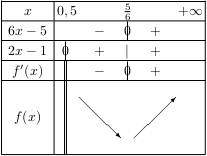
Et par là, $f$ admet pour minimum $f({5}/{6})=3×{5}/{6}-\ln (2×{5}/{6}-1)=2,5-\ln {2}/{3}$.
Propriétés
La fonction $\ln x$ est continue sur $]0;+∞[$.
$\ln x$ est strictement négative sur $]0;1[$.
$\ln x$ est strictement positive sur $]1;+∞[$.
La fonction $\ln x$ est strictement croissante.
Exemple
Soit $\C$ la courbe représentative de $\ln x$.
Déterminer une équation de $d_0$, tangente à $C$ en 1.
Déterminer une équation de $d_1$, tangente à $C$ en e.
Corrigé
Posons $f(x)=\ln x$. On a donc: $f\,'(x)={1}/{x}$.
$d_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=1$, $f(x_0)=\ln 1=0$, $f\,'(x_0)={1}/{1}=1$.
D'où l'équation: $y=0+1(x-1)$, soit: $y=x-1$.
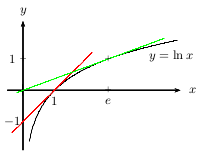
Donc finalement, $d_0$ a pour équation: $y=x-1$ (elle est tracée en rouge sur le dessin de la propriété précédente).
$d_1$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=e$, $f(x_1)=\ln e=1$, $f\,'(x_1)={1}/{e}$.
D'où l'équation: $y=1+{1}/{e}(x-e)$, soit: $y=1+{1}/{e}x-1$, soit: $y={1}/{e}x$.
Donc finalement, $d_1$ a pour équation: $y={1}/{e}x$ (elle est tracée en vert sur le dessin de la propriété précédente).
Exemple
Sans calculatrice, donner le signe de $\ln 0,5$, de $\ln 1,9$.
Corrigé
$0,5\text"<"1$, et donc $\ln 0,5\text"<"0$.
$1,9\text">"1$, et donc $\ln 1,9\text">"0$.
Limites de référence
$\lim↙{x→+∞}\ln x=+∞$ $\lim↙{x→0}\ln x=-∞$
 Exemple
Exemple
Déterminer $\lim↙{x→+∞}\ln (x)+x^2+5$.
Déterminer $\lim↙{x→0}\ln (2x+3)+\ln x$.
Corrigé
On a $\lim↙{x→+∞}\ln (x)=+∞$
Et $\lim↙{x→+∞}x^2=+∞$
Et $\lim↙{x→+∞}5=5$.
Donc $\lim↙{x→+∞}\ln (x)+x^2+5=+∞$ (limite d'une somme).
On a $\lim↙{x→0}\ln (2x+3)=2×0+3=3$.
Et $\lim↙{x→0}\ln x=-∞$
Donc $\lim↙{x→0}\ln (2x+3)+\ln x=-∞$ (limite d'une somme).
Propriétés
Pour tous nombres réels strictement positifs $a$ et $b$, pour tout entier relatif $p$, on a:
$\ln ab=\ln a+\ln b$
$\ln {a}/{b}=\ln a-\ln b$
$\ln a^p=p\ln a$
$\ln √a={1}/{2}\ln a$
Pour tous nombre réel $a$ , on a: $\ln (e^a)=a$
Pour tous nombre réel strictement positif $a$ , on a:
$e^{\ln a}=a$
Exemple
Simplifier les expressions suivantes: $A=3\ln 2-\ln4+\ln(e^{1,19})$ $B=\ln x^2-\ln x+e^{\ln3,7}$.
Corrigé
$A=3\ln 2-\ln4+\ln(e^{1,19})=\ln 2^3-\ln4+1,19=\ln8-\ln4+1,19$.
Soit: $A=\ln{8}/{4}+1,19=\ln2+1,19$.
$B=\ln x^2-\ln x+e^{\ln3,7}=\ln{x^2}/{x}+3,7=\ln x+3,7$.
Propriétés
Pour tous nombres réels strictement positifs $a$ et $b$, on a:
$\ln a\text"<"\ln b ⇔ a\text"<"b$ et $\ln a=\ln b ⇔ a=b$
 Exemple
Exemple
- Résoudre l'équation $\ln(x-2)=0$.
- Résoudre l'inéquation $\ln(-5x+3)-1≤0$.
- Résoudre l'inéquation $\ln(-5x+3)≤4$.
- Résoudre l'inéquation $e^(-4x)-7≤0$.
- Résoudre l'inéquation $5×0,98^n≤0,9$ où $n$ est un entier naturel.
Corrigé
-
On doit avoir $x-2\text">"0$, soit $x\text">"2$. Donc $\D_E=]2;+∞[$.
$\ln(x-2)=0⇔\ln(x-2)=\ln 1⇔x-2=1⇔x=3$.
Autre méthode: $\ln(x-2)=0⇔e^{\ln(x-2)}=e^0⇔x-2=1⇔x=3$.
Donc $\S=\{3\}$. Notons que 3 est bien dans $\D_E$ -
On doit avoir $-5x+3\text">"0$, soit $-5x\text">"-3$, soit $x\text"<"{-3}/{-5}$, soit $x\text"<"0,6$.
Donc $\D_E=]-∞;0,6[$.
(E)$⇔\ln(-5x+3)-1≤0⇔\ln(-5x+3)≤1$
Soit: (E) $⇔\ln(-5x+3)≤\ln e⇔-5x+3≤e$
Autre méthode: (E)$⇔e^{\ln(-5x+3)}≤e^1⇔-5x+3≤e$
Soit: (E)$⇔-5x≤e-3⇔x≥{e-3}/{-5}$
Donc $\S=[{e-3}/{-5};0,6[$. Notons que ${e-3}/{-5}≈0,06$. -
On doit avoir $-5x+3\text">"0$, soit $-5x\text">"-3$, soit $x\text"<"{-3}/{-5}$, soit $x\text"<"0,6$.
Donc $\D_E=]-∞;0,6[$.
$\ln(-5x+3)≤4⇔e^{\ln(-5x+3)}≤e^4⇔-5x+3≤e^4⇔-5x≤e^4-3⇔x≥{e^4-3}/{-5}$
Donc $\S=[{e^4-3}/{-5};0,6[$. Notons que ${e^4-3}/{-5}≈-10,32$. -
$\D_E=\R$
$e^(-4x)-7≤0⇔e^(-4x)≤7⇔\ln(e^(-4x))≤\ln 7⇔-4x≤\ln 7⇔x≥{\ln 7}/{-4}$.
Donc $\S=[{\ln 7}/{-4};+∞[$. Notons que ${\ln 7}/{-4}≈-0,49$. -
$\D_E$ est l'ensemble des entiers naturels.
(E)$⇔5×0,98^n≤0,9⇔0,98^n≤{0,9}/{5}⇔0,98^n≤0,18⇔\ln0,98^n≤\ln 0,18$
Soit: (E)$⇔n\ln0,98≤\ln 0,18$.
Soit: (E)$⇔n≥{\ln 0,18}/{\ln0,98}$.
Notons le changement de sens de l'inégalité car $\ln 0,98\text"<"0$.
On a: ${\ln 0,18}/{\ln0,98}≈84,88$.
Donc, finalement, $\S$ est l'ensemble des entiers supérieurs ou égaux à $85$.
Savoir faire
Comment résoudre les équations et les inéquations où apparait la fonction $\ln$ ou la fonction exponentielle?
En général, il suffit d'isoler le terme contenant la fonction problématique,
puis de composer chaque membre de l'équation ou de l'inéquation par la fonction réciproque.
Ne pas oublier de déterminer le domaine d'étude, en particulier quand la fonction $\lb$ intervient!
(lire l'exemple ci-dessus)