 Annales
Annales
Afrique 2013
Exercice 1
6 points Commun à tous les candidats
Un industriel fabrique des vannes électroniques destinées à des circuits hydrauliques.
Les 4 parties A, B, C et D sont indépendantes.
Partie A
La durée de vie d'une vanne, exprimée en heures, est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $λ=0,0002$.
- Quelle est la durée de vie moyenne d'une vanne?
- Calculer la probabilité, à 0,001 près, que la durée de vie d'une vanne soit supérieure à 6000 heures.
Partie B
Avec 3 vannes identiques $V_1$, $V_2$, $V_3$, on fabrique le circuit hydraulique ci-dessous.
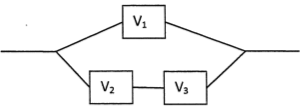
Le circuit est en marche si $V_1$ est en état de marche ou si $V_2$ et $V_3$ le sont simultanément.
On assimile à une expérience aléatoire le fait que chaque vanne est ou n'est pas en état de marche après 6000 heures. On note:
$F_1$ l'événement: " la vanne $V_1$ est en état de marche après 6000 heures".
$F_2$ l'événement: " la vanne $V_2$ est en état de marche après 6000 heures".
$F_3$ l'événement: " la vanne $V_3$ est en état de marche après 6000 heures".
$E$ l'événement: " le circuit est en état de marche après 6000 heures".
On admet que les événements $F_1$, $F_2$ et $F_3$ sont 2 à 2 indépendants et ont chacun une probabilité égale à 0,3.
- L'arbre probabiliste ci-dessous représente une partie de la situation.
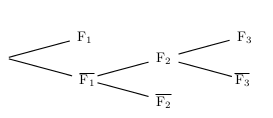
Reproduire l'arbre probabiliste ci-dessus et placer les probabilités sur les branches. - Démontrer que $p(E)=0,363$.
- Sachant que le circuit est en état de marche aprés 6000 heures, calculer la probabilité que la vanne $V_1$ soit en état de marche à ce moment là. Arrondir au millième.
Partie C
L'industriel affirme que seulement $2%$ des vannes qu'il fabrique sont défectueuses. On supose que cette affirmation est vraie,
et l'on note $F$ la variable aléatoire égale à la fréquence de vannes défectueuses dans un échantillon aléatoire de 400 vannes prises dans la production totale.
- Déterminer l'intervalle $I$ de fluctuation asymptotoque au seuil de $95%$ de la variable $F$.
- On choisit 400 vannes au hasard dans la production. On assimile ce choix à un tirage aléatoire de 400 vannes, avec remise, dans la production.
Parmi ces vannes, 10 sont défectueuses.
Au vu de ce résultat, peut-on remettre en cause, au seuil de $95%$, l'affirmation de l'industriel?
Partie D
Dans cette partie, les probabilités seront arrondies au millième.
L'industriel commercialise ses vannes auprès de nombreux clients.
La demande mensuelle est une variable aléatoire $D$ qui suit
la loi normale d'espérance $m=800$ et d'écart-type $σ=40$.
- Déterminer $p(760≤D≤840)$.
- Déterminer $p(D≤880)$.
- L'industriel pense que s'il constitue un stock mensuel de 880 vannes, il n'aura pas plus de $1%$ de chance d'être en rupture de stock. A-t-il raison?
Corrigé de l'exercice 1
- $T$ donne la durée de vie d'une vanne (en heures). Donc la durée de vie moyenne d'une vanne est l'espérance $E$ de $T$.
Or $T$ suit la loi exponentielle de paramètre $λ=0,0002$. Donc son espérance est $E={1}/{λ}={1}/{0,0002}=5000$.
Par conséquent, la durée de vie d'une vanne est égale à 5000 heures. - On cherche $p(6000≤T)=e^{-λ6000}=e^{-0,0002×6000}≈0,301$.
Donc la probabilité que la durée de vie d'une vanne soit supérieure à 6000 heures est d'environ $0,301$.
Partie B
- Ci-dessous l'arbre probabiliste complété.
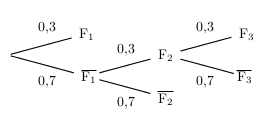
- $E=F_1 ∪ (\ov{F_1}∩F_2∩F_3)$. Or, les événements $F_1$ et $\ov{F_1}∩F_2∩F_3$ sont incompatibles. Donc $p(E)=p(F_1)+p(\ov{F_1}∩F_2∩F_3)$.
Or, d'après l'arbre précédent, on a: $p(F_1)=0,3$ et $p(\ov{F_1}∩F_2∩F_3)=0,7×0,3×0,3=0,063$.
Par conséquent: $p(E)=0,3+0,063=0,363$. Soit: $p(E)=0,363$. - On cherche $p_E(F_1)$.
On a: $p_E(F_1)={p(E∩F_1)}/{p(E)}$.
Or: $E∩F_1=F_1$. Et par là: $p(E∩F_1)=p(F_1)=0,3$.
Et on a vu que $p(E)=0,363$.
Donc $p_E(F_1)={0,3}/{0,363}≈0,826$. Soit: $p_E(F_1)≈0,826$.
Partie C
-
Avec les notations usuelles, on pose: $n=400$, $p=0,02$.
$p-1,96{√{p(1-p)}}/{√{n}}=0,02-1,96{√{0,02×0,98}}/{√{400}}=0,00628$.
$p+1,96{√{p(1-p)}}/{√{n}}=0,02+1,96{√{0,02×0,98}}/{√{400}}=0,03372$.
L'intervalle de fluctuation asymptotique au seuil de $95\%$ de $F$ vaut $[0,00628;0,03372]$. - L'industriel affirme que seulement $2%$ des vannes qu'il fabrique sont défectueuses.
On se demande si l'hypothèse $p=0,02$ est correcte.
Tout d'abord, on a: $n≥30$.
De plus: $np=8$ et $n(1-p)=392$; et par là: $np≥5$ et $n(1-p)≥5$.
L'intervalle de fluctuation asymptotique peut donc être utilisé.
La fréquence de vannes défectueuses est égale à ${10}/{400}=0,025$.
Cette fréquence est dans l'intervalle de fluctuation asymptotique au seuil de $95\%$ de $F$.
Donc on ne peut pas remettre en cause, au seuil de $95%$, l'affirmation de l'industriel.
Partie D
- A la calculatrice, on obtient: $p(760≤D≤840)≈0,683$ (méthode ici).
- A la calculatrice, on obtient: $p(D≤880)≈0,977$ (méthode ici).
- Comme $p(D≤880)≈0,977$, on en déduit que $p(D$>$880)≈2,3%$.
Et par là, avec un stock mensuel de 880 vannes,l'industriel aura plus de $1%$ de chance d'être en rupture de stock.
L'industriel a donc tort!
Exercice 2
4 points Commun à tous les candidats
Les 4 questions sont indépendantes.
Pour chacune, une affirmation est proposée. Indiquer si elle est vraie ou fausse, en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte.
Dans l'espace muni d'un repère orthonormé, on considère
- les points $A(12,0,0)$, $B(0,-15,0)$, $C(0,0,20)$, $D(2,7,-6)$ et $E(7,3,-3)$.
- le plan $P$ d'équation cartésienne $2x+y-2z-5=0$
Affirmation 1
Une équation cartésienne du plan parallèle à $P$ et passant par le point A est $2x+y+2z-24=0$.
Affirmation 2
Une représentation paramétrique de la droite (AC) est $\{\table x=9-3t; y=0;z=5+5t$.
Affirmation 3
La droite (DE) et le plan $P$ ont au moins un point commun.
Affirmation 4
La droite (DE) est orthogonale au plan (ABC).
Solution...
Corrigé de l'exercice 2
L'affirmation 1 est fausse.
En effet: si le plan d'équation cartésienne $2x+y+2z-24=0$ passe effectivement par A (car $2x_A+y_A+2z_A-24=0$), il n'est pas parallèle à $P$.
Prouvons le.
On rappelle que deux plans de vecteurs normaux respectifs ${n}↖{→}$ et ${n}↖{→}$ sont parallèles
si et seulement si ${n}↖{→}$ et ${n'}↖{→}$ sont colinéaires.
Or, ici, $P$ d'équation cartésienne $2x+y-2z-5=0$ admet pour vecteur normal ${n}↖{→}(2;1;-2)$,
et le plan d'équation cartésienne $2x+y+2z-24=0$ admet pour vecteur normal ${n'}↖{→}(2;1;2)$.
Et comme ${n}↖{→}$ et ${n'}↖{→}$ ne sont pas colinéaires (aucun n'est nul et leurs coordonnées ne sont pas proportionnelles),
les 2 plans ne sont pas parallèles.
Finalement, une équation cartésienne du plan parallèle à $P$ et passant par le point A n'est pas $2x+y+2z-24=0$.
L'affirmation 2 est vraie.
Démonstration: il suffit de prouver que $d$, droite de représentation paramétrique $\{\table x=9-3t; y=0;z=5+5t$, passe par A et est parallèle à $(AC)$.
A( 12 ; 0 ; 0 ) est sur $d$ si et seulement si
il existe un réel $t$ tel que $\{\table 12=9-3t; 0=0;0=5+5t$
Or $\{\table 12=9-3t; 0=0;0=5+5t$ $⇔$ $\{\table 3=-3t; 0=0; -1=t$$ ⇔$ $\{\table -1=t; 0=0; -1=t$
Donc $t$ existe et vaut $-1$, et par là, A est bien sur $d$.
Par ailleurs, $d$ a pour vecteur directeur ${u}↖{→}$( -3 ; 0 ; 5 ).
Et (AC) a pour vecteur directeur ${AC}↖{→}$( -12 ; 0 ; 20 ).
On note alors que ${AC}↖{→}=4{u}↖{→}$. Les deux vecteurs directeurs sont donc colinéaires, et par là, les droites sont bien parallèles.
Finalement, ne représentation paramétrique de la droite (AC) est bien $\{\table x=9-3t; y=0;z=5+5t$.
L'affirmation 3 est fausse.
Démonstration: il suffit de montrer que ni D, ni E n'est sur $P$.
On a: $2_D+y_D-2z_D-5=2×2+7-2×(-6)-5=18$.
Donc $2_D+y_D-2z_D-5≠0$, donc $D∉P$.
On a: $2_E+y_E-2z_E-5=2×7+3-2×(-3)-5=18$.
Donc $2_E+y_E-2z_E-5≠0$, donc $E∉P$.
Finalement, la droite (DE) et le plan $P$ n'ont pas de point commun.
L'affirmation 4 est vraie.
Démonstration:
Le plan (ABC) a pour vecteurs directeurs ${AB}↖{→}$( -12 ; -15 ; 0 ) et ${AC}↖{→}$( -12 ; 0 ; 20 ).
La droite (DE) a pour vecteur directeur ${DE}↖{→}$( 5 ; -4 ; 3 ).
${AB}↖{→}.{DE}↖{→}=(-12)×5+(-15)×(-4)+0×3=0$.
${AC}↖{→}.{DE}↖{→}=(-12)×5+0×(-4)+20×3=0$.
Par conséquent, la droite (DE) est orthogonale au plan (ABC).
Exercice 3
5 points Commun à tous les candidats
On considère la fonction $g$ définie pour tout réel $x$ de l'intervalle $[0;1]$ par $g(x)=1+e^{-x}$.
On admet que, pour tout réel $x$ de l'intervalle $[0;1]$, $g(x)≥0$.
On note $C$ la courbe représentative de $g$ dans un repère orthogonal, et $D$ le domaine du plan compris d'une part entre l'axe des abscisses et la courbe $C$, d'autre part entre les droites d'équations $x=0$ et $x=1$.
La courbe $C$ et le domaine $D$ sont représentés ci-dessous.
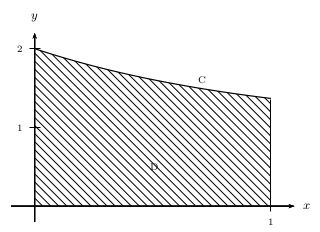
Le but de cet exercice est de partager le domaine $D$ en 2 domaines de même aire, d'abord par une droite parallèle à l'axe des abscisses (partie A), puis par une droite parallèle à l'axe des ordonnées (partie B).
Partie A
Soit $a$ un réel tel que $0≤a≤1$.
On note $A_1$ l'aire du domaine compris entre $C$, l'axe des abscisses, les droites d'équations $x=0$ et $x=a$.
On note $A_2$ l'aire du domaine compris entre $C$, l'axe des abscisses, les droites d'équations $x=a$ et $x=1$.
$A_1$ et $A_2$ sont exprimées en unités d'aires.
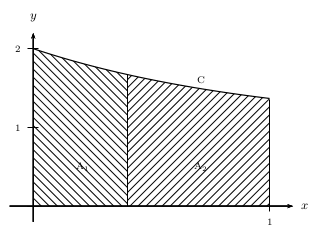
-
- Démontrer que $A_1=a-e^{-a}+1$.
- Exprimer $A_2$ en fonction de $a$.
- Soit $f$ la fonction définie pour tout réel $x$ de l'intervalle $[0;1]$ par $f(x)=2x-2e^{-x}+{1}/{e}$.
- Dresser le tableau de variation de la fonction $f$ sur l'intervalle $[0;1]$. On précisera les valeurs exactes de $f(0)$ et de $f(1)$.
- Démontrer que la fonction $f$ s'annule une fois et une seule sur l'intervalle $[0;1]$ en un réel $α$. Donner la valeur de $α$ arrondie au centième.
- En utilisant les questions précédentes, déterminer une valeur approchée du réel $a$ pour lequel les aires $A_1$ et $A_2$ sont égales.
Partie B
Soit $b$ un réel positif.
Dans cette partie, on se propose de partager le domaine $D$ en 2 domaines de même aire par la droite d'équation $y=b$. On admet qu'il existe un unique réel positif $b$ solution.
- Justifier l'inégalité $b$<$1+{1}/{e}$. On pourra utiliser un argument graphique.
- Déterminer la valeur exacte de $b$.
Solution...
Corrigé de l'exercice 3
Partie A
-
- La fonction $g$, clairement dérivable, est donc continue.
De plus, il est admis que $g$ est positive sur $[0;1]$, donc elle l'est sur $[0;a]$ car $0≤a≤1$.
Par conséquent, $$A_1=∫_0^a g(t)dt$$
Soit: $$A_1=∫_0^a (1+e^{-t})dt=[t-e^{-t}]_0^a=a-e^{-a }-(0-e^{-0})=a-e^{-a}+1$$.
Soit: $$A_1=a-e^{-a}+1$$. - De même, on obtient: $$A_2=∫_a^1 g(t)dt=[t-e^{-t}]_a^1=1-e^{-1}-(a-e^{-a })=-a+e^{-a}+1-e^{-1}$$.
Soit: $$A_2=-a+e^{-a}+1-e^{-1}$$.
- La fonction $g$, clairement dérivable, est donc continue.
-
- $f\,'(x)=2-2e^{-x}(-1)+0=2+2e^{-x}$.
$f\,'(x)$ est donc une somme de 2 termes strictement positifs, et par là, $f\,'(x)$ est strictement positif, et c'est vrai pour tout $x$ de $[0;1]$.
Donc $f$ est strictement croissante, d'où le tableau de variation de la fonction $f$ sur l'intervalle $[0;1]$.
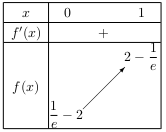
On note que: $f(0)=0-2e^{0}+{1}/{e}={1}/{e}-2≈-1,6$ et $f(1)=2-2e^{-1}+{1}/{e}=2-2{1}/{e}+{1}/{e}=2-{1}/{e}≈1,6$ -
D'après le tableau de variation ci-dessus, la fonction $f$ est continue et strictement croissante sur $\[0;1\]$.
Or 0 est un nombre compris entre $f(0)$ et $f(1)$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=0$ admet une unique solution $α$ sur $\[0;1\]$.
Nous déterminons $α$ par essais successifs.

Donc $α≈0,45$ (arrondie au centième).
- $f\,'(x)=2-2e^{-x}(-1)+0=2+2e^{-x}$.
- D'après le 1., les aires $A_1$ et $A_2$ sont égales pour $a$ solution de l'équation: $a-e^{-a}+1=-a+e^{-a}+1-e^{-1}$.
Soit: $a-e^{-a}+1+a-e^{-a}-1+e^{-1}=0$.
Soit: $2a-2e^{-a}+e^{-1}=0$.
Soit: $f(a)=0$.
Donc, d'après le 2., les aires $A_1$ et $A_2$ sont égales pour $a≈0,45$ (arrondie au centième).
Partie B
- Notons que $g(1)=1+{1}/{e}$.
Pour $b$=$1+{1}/{e}$, le domaine $D$ se partage alors selon le dessin suivant.
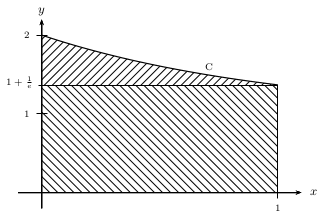
Il est graphiquement évident que les aires des 2 sous domaines ne sont pas égales, et que cela sera pire encore si $b$>$1+{1}/{e}$. Donc $b$<$1+{1}/{e}$. - D'après la question précédente, le domaine doit donc se partager en 2 sous domaines dont l'un d'eux est un rectangle R de côtés 1 et $b$, et donc d'aire $b$.
Or, l'aire totale de $D$ est $A_1+A_2=a-e^{-a}+1-a+e^{-a}+1-e^{-1}=2-{1}/{e}$.
La moitié de cette aire vaut donc $A_{m}={1}/{2}(2-{1}/{e})=1-{1}/{2e}$.
C'est la valeur exacte de $b$ cherchée.
On a donc $b=1-{1}/{2e}$.
Pour le plaisir, notons alors le partage équitable obtenu ci-dessous.
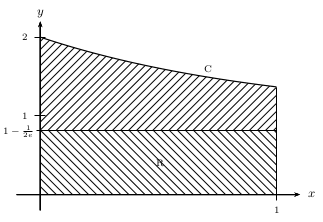
Exercice 4
5 points Candidats n'ayant pas suivi l'enseignement de spécialité
L'objet de cet exercice est l'étude de la suite $(u_n)$ définie par son premier terme $u_1={3}/{2}$ et par la relation de récurrence $u_{n+1}={nu_n+1}/{2(n+1)}$.
PARTIE A - Algorithmique et conjectures
Un élève propose l'algorithme suivant, dans lequel il a oublié de compléter 2 lignes.
$n$ ← 1
$u$ ← 1,5
Tant que $n$<$9$
$u$ ← ...
$n$ ← ...
Fin tant que
A la fin de l'exécution de cet algorithme, le terme $u_9$ de la suite sera contenu dans la variable $u$.
- Recopier et compléter les 2 lignes de l'algorithme où figurent les points de suspension.
- Comment faudrait-il modifier l'algorithme pour qu'il calcule et affiche tous les termes de la suite de $u_2$ à $u_9$?
Rappelons que, pour afficher la valeur contenue dans une variable $x$, il suffit d'ajouter l'instruction: "afficher $x$".
- Avec cet algorithme modifié, on a obtenu les résultats suivants, arrondis au dix-millième.

Au vu de ces résultats, conjecturer le sens de variation et la convergence de la suite $(u_n)$.
PARTIE B - Etude mathématique
On définit la suite auxiliaire $(v_n)$ par: pour tout entier $n$, $v_n=nu_n-1$.
- Montrer que la suite $(v_n)$ est géométrique; préciser sa raison et son premier terme.
- En déduire que, pour tout entier $n≥1$, on a: $u_n={1+0,5^n}/{n}$.
- Déterminer la limite de la suite $(u_n)$.
- Justifier que, pour tout entier $n≥1$, on a: $u_{n+1}-u_n=-{1+(1+0,5n)0,5^n}/{n(n+1)} $.
En déduire le sens de variation de la suite $(u_n)$.
PARTIE C - Retour à l'algorithmique
En s'inspirant de la partie A, écrire un algorithme permettant de déterminer
le plus petit entier $n$ tel que $u_n$<$0,001$.
Préciser dans quelle variable sera contenue la valeur de $n$ cherchée à la fin de l'exécution de l'algorithme.
Solution...
Corrigé de l'exercice 4
PARTIE A - Algorithmique et conjectures
- Algorithme complété:
$n$ ← 1.
$u$ ← 1,5
Tant que $n$<$9$
$u$ ← $(n×u)/(2×(n+1)$
$n$ ← $n+1$
Fin tant que
- Algorithme modifié en rajoutant la ligne "Afficher $u$" :
$n$ ← 1.
$u$ ← 1,5
Tant que $n$<$9$
$u$ ← $(n×u)/(2×(n+1)$
Afficher $u$
$n$ ← $n+1$
Fin tant que
On notera que $u_1$ n'est pas affiché, et que $u_9$ ne s'affiche qu'une fois.
Pour que $u_1$ s'affiche également, on aurait pu modifier l'algorithme comme suit:
$n$ ← 1.
$u$ ← 1,5
Tant que $n$<$9$
Afficher $u$
$u$ ← $(n×u)/(2×(n+1)$
$n$ ← $n+1$
Fin tant que
Afficher $u$
- Compte tenu du tableau de valeurs proposé, il semble que la suite $(u_n)$ soit strictement décroissante et tende vers 0.
PARTIE B - Etude mathématique
On définit la suite auxiliaire $(v_n)$ par: pour tout entier $n$, $v_n=nu_n-1$.
- Soit $n$ un entier naturel.
$v_{n+1}=(n+1)u_{n+1}-1=(n+1){nu_n+1}/{2(n+1)}-1={(n+1)(nu_n+1)-2(n+1)}/{2(n+1)}$
Soit: $v_{n+1}={(n+1)nu_n+(n+1)-2(n+1)}/{2(n+1)}={(n+1)nu_n-(n+1)}/{2(n+1)}={(n+1)(nu_n-1)}/{2(n+1)}={nu_n-1}/{2}$
Soit: $v_{n+1}={1}/{2}v_n$.
Et c'est vrai pour tout entier naturel $n$.
Donc la suite $(v_n)$ est géométrique de raison ${1}/{2}$. Son premier terme est $v_1=1×u_1-1={3}/{2}-1={1}/{2}$. - Soit $n$ un entier naturel non nul.
$v_n=nu_n-1$ donne $u_n={v_n+1}/{n}$.
Or, comme $(v_n)$ est géométrique de raison ${1}/{2}$ de premier terme $v_1={1}/{2}$, on a: $v_n={1}/{2}×({1}/{2})^{n-1}=0,5^n$.
Donc on obtient: $u_n={0,5^n+1}/{n}$. Soit: $u_n={1+0,5^n}/{n}$. - Comme $0$<$0,5$<$1$, on a: $\lim↙{n→+∞}{0,5^n}=0$, et par là: $\lim↙{n→+∞}{1+0,5^n}=1+0,5×0=1$.
Et comme $\lim↙{n→+∞}{n}=+∞$, on obtient finalement: $\lim↙{n→+∞}{(u_n)}=0$. - Soit $n$ un entier naturel non nul.
$u_{n+1}-u_n= {1+0,5^{n+1}}/{n+1}-{1+0,5^n}/{n}={n(1+0,5^{n+1})-(n+1)(1+0,5^n)}/{n(n+1)}$
Soit: $u_{n+1}-u_n={n+n0,5^{n+1}-(n+1)-(n+1)0,5^n}/{n(n+1)}={n+(0,5n-n-1)0,5^{n}-n-1}/{n(n+1)}$
Soit: $u_{n+1}-u_n={(-0,5n-1)0,5^{n}-1}/{n(n+1)}=-{1+(1+0,5n)0,5^n}/{n(n+1)} $.
$n$ étant un entier naturel non nul, numérateur et dénominateur du quotient ci-dessus sont strictement positifs.
Et par là, $u_{n+1}-u_n$ est strictement négatif.
Ceci étant vrai pour tout entier $n≥1$, on en déduit que la suite $(u_n)$ est strictement décroissante.
PARTIE C - Retour à l'algorithmique
Voici un algorithme convenable:
$n$ ← 1.
$u$ ← 1,5
Tant que $u≥0,001$
$u$ ← $(n×u)/(2×(n+1)$
$n$ ← $n+1$
Fin tant que
A la fin de l'exécution de cet algorithme, la valeur de $n$ cherchée sera contenue dans la variable $n$.