 Dérivées, convexité
Dérivées, convexité
A SAVOIR: le cours sur Dérivées, convexité
Exercice 1
Cet exercice utilise exclusivement des fonctions vues en première.
Déterminer $f\,'$, puis le signe de $f\,'$ sur I, et dresser alors le tableau de variation de $f$ sur l'intervalle I (sans les limites) dans chacun des cas suivants:
- $f(x)=√{x}+x^3+x$ sur $I=]0;+∞[$
- $f(x)=-5x^2+x+3$ sur $I=\R$
- $f(x)=8x^2-x+9$ sur $I=[0;{1}/{16}]$
- $f(x)=-x^3+{3}/{2}x^2$ sur $I=\R$
- $f(x)=-2x^3-0,5x^2+x+3$ sur $\R$
- $f(x)={x^2}/{2x+1}$ sur $I=[-1;-0,5[$
Corrigé
- $f(x)=√{x}+x^3+x$ sur $I=]0;+∞[$.
$f\,'(x)={1}/{2√{x}}+3x^2+1$.
$f\,'$ est une somme de termes.
Les termes ${1}/{2√{x}}$ et $3x^2$ sont positifs, le terme 1 est strictement positif.
Donc $f\,'$ est strictement positive sur $I=]0;+∞[$.
D'où le tableau de variation de $f$ sur I.
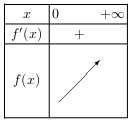
- $f(x)=-5x^2+x+3$ sur $I=\R$.
$f\,'(x)=-5×2x+1+0=-10x+1$.
$f\,'$ est une fonction affine de coefficient $-10$ strictement négatif.
On note que: $-10x+1=0⇔-10x=-1⇔x={-1}/{-10}=0,1$.
D'où le tableau de variation de $f$ sur I.
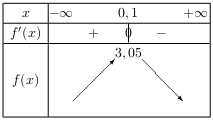
- $f(x)=8x^2-x+9$ sur $I=[0;{1}/{16}]$.
$f\,'(x)=8×2x-1+0=16x-1$.
$f\,'$ est une fonction affine de coefficient $16$ strictement positif.
On note que: $16x-1=0⇔16x=1⇔x={1}/{16}$.
D'où le tableau de variation de $f$ sur I.
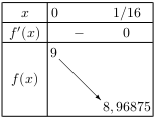
- $f(x)=-x^3+{3}/{2}x^2$ sur $I=\R$.
$f\,'(x)=-3x^2+{3}/{2}2x=-3x^2+3x=-3x(x-1)$.
$f\,'$ est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier).
$-3x$ a pour coefficient $-3$ strictement négatif.
$x-1$ a pour coefficient $1$ strictement positif.
On note que: $-3x=0⇔x={0}/{-3}=0$.
On note que: $x-1=0⇔x=1$.
D'où le tableau de variation de $f$ sur I.
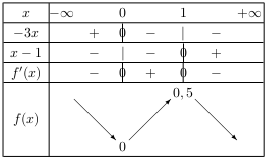
-
$f(x)=-2x^3-0,5x^2+x+3$ sur $\R$.
$f\,'(x)=-2×3x^2-0,5×2x+1=-6x^2-x+1$.
$f\,'$ est un trinôme avec $a=-6$, $b=-1$ et $c=1$.
$Δ=b^2-4ac=(-1)^2-4×(-6)×1=25$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-5}/{-12}={1}/{3}$ et $x_2={-b+√Δ}/{2a}={1+5}/{-12}=-0,5$.
$a\text"<"0$. D'où le tableau suivant:
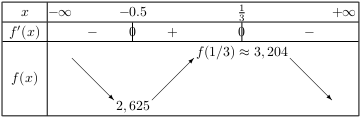
- $f(x)={x^2}/{2x+1}$ sur $I=[-1;-0,5[$.
On pose $f={u}/{v}$ avec $u=x^2$ et $v=2x+1$.
D'où $f\,'={u'v-uv'}/{v^2}$ avec $u'=2x$ et $v'=2$.
Soit $f\,'(x)={2x×(2x+1)-x^2×2}/{(2x+1)^2}={4x^2+2x-2x^2}/{(2x+1)^2}={2x^2+2x}/{(2x+1)^2}={2x(x+1)}/{(2x+1)^2}$.
Le numérateur est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier).
$2x$ a pour coefficient $2$ strictement positif.
$x+1$ a pour coefficient $1$ strictement positif.
On note que: $2x=0⇔x={0}/{2}=0$.
On note que: $x+1=0⇔x=-1$.
Le dénominateur est un carré strictement positif pour $x≠-0,5$.
D'où le tableau de variation de $f$ sur I.
