Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 1
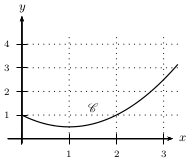
Soit $f$ de courbe représentative $C$ dans un repère orthogonal.
Soit $$A=∫_{1}^3 f(t)dt$$.
Déterminer graphiquement quel encadrement est correct:
- $1≤A≤2$
- $2≤A≤3$
- $3≤A≤4$
Corrigé
$f$ est clairement continue et positive sur $[1;3]$.
Et de ce fait $A$ est l'aire du domaine $D=${$M(x;y)$/$1≤x≤3$ et $0≤y≤f(x)$}.
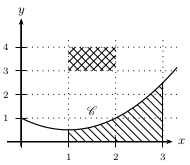
Il suffit donc de déterminer graphiquement l'aire de la partie hachurée sous la courbe ci-dessous.
Rappelons que cette aire est exprimée en unités d'aires. D'ailleurs, une unité d'aire est visualisée par le rectangle situé au dessus de la courbe
Il suffit donc de compter combien de rectangles donnent la même aire que celle de $D$.
La réponse correcte est donc: $2≤A≤3$