 Fonction logarithme népérien
Fonction logarithme népérien
A SAVOIR: le cours sur équations, inéquations et fonction ln
Exercice 5
Soit $f$ définie sur $[{1}/{e};e]$ par $f(x)=x^2+x-3\ln x$.
1. Déterminer $f\,'(x)$, étudier son signe, et dresser le tableau de variation de $f$ sur $[{1}/{e};e]$.
2. Montrer que l'équation $f(x)=4$ admet une solution unique $s$ sur l'intervalle $[1;e]$.
3. Recopier l'algorithme suivant, et compléter les 2 lignes incomplètes pour que,
à la fin de son exécution, les variables A et B fournissent un encadrement d'amplitude $0,01$ de la solution $s$.
$A$ ← $1$
$B$ ← $e$
$L$ ← $4$
$D$ ← $0,01$
Tant que ...
Si $f({A+B}/{2})...$
Alors $B$ ← ${A+B}/{2}$
Sinon $A$ ← ${A+B}/{2}$
Fin du Si
Fin du Tant que
Corrigé
1. Dérivons $f(x)$
Donc $f\,'(x)=2x+1-3{1}/{x}={2x^2}/{x}+{x}/{x}-{3}/{x}={2x^2+x-3}/{x}$.
Le numérateur est un trinôme avec $a=2$, $b=1$ et $c=-3$. $Δ=b^2-4ac=1^2-4×2×(-3)=1+24=25$.
$Δ\text">"0$. Le trinôme a 2 racines.
$x_1={-b-√Δ}/{2a}={-1-5}/{4}=-1,5$ (hors intervalle) et $x_2={-b+√Δ}/{2a}={-1+5}/{4}=1$.
Le trinôme est du signe de $a$ (positif) à l'extérieur des racines.
Le dénominateur est strictement positif sur $\R+$, et donc sur $[{1}/{e};e]$.
D'où le tableau de signes de $f\,'$ et de variation de $f$.
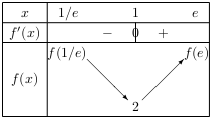
On note que: $f(1)=1^2+1-3\ln1=1+1-3×0=2$
$f({1}/{e})=({1}/{e})^2+{1}/{e}-3\ln{1}/{e}={1}/{e^2}+{1}/{e}-3(\ln1-\ln e)={1}/{e^2}+{1}/{e}-3(0-1)={1}/{e^2}+{1}/{e}+3≈3,5$
$f(e)=e^2+e-3\ln e=e^2+e-3×1=e^2+e-3≈7,1$
2. D'après le tableau de variation, la fonction $f$ est continue et strictement croissante sur $\[1;e]$.
Or 4 est un nombre compris entre $f(1)=2$ et $f(e)≈7,1$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=4$ admet une unique solution sur $\[1;e]$.
3. ALGORITHME COMPLET:
$A$ ← $1$
$B$ ← $e$
$L$ ← $4$
$D$ ← $0,01$
Tant que $B-A$>$D$
Si $f({A+B}/{2})>L$
Alors $B$ ← ${A+B}/{2}$
Sinon $A$ ← ${A+B}/{2}$
Fin du Si
Fin du Tant que